题目的来源

先来说说题目的来源，这是帮外国留学生做的一个作业题目，其实很多时候我都会先去chegg这个相当于外国作业帮的地方搜，要是没有再自己做，一般也学不到啥，但是今天遇到一个搜不到又不得不做的题，和同学们请教后也是终于明白了，决定写一篇博客和大家分享一下。

题目

嗯我们先贴一下英文版和我翻译后的中文版题目吧，内容确实蛮长的，我会尽可能用简单的方式让不太了解其中定义的朋友们也看懂。

Let G = (V, E) be a directed, weighted graph (edge weights are allowed to be negative). For any subset of edges S ⊂ E, we let G − S = (V, E − S), denote the graph G with all the edges of S removed.

English version:

Consider the following problem
• INPUT:
– A directed, weighted graph G (edge weights are allowed to be negative), and a single edge (a, b) such that G− {(a, b)} is a DAG; that is, if you remove edge (a, b) from G, then the resulting graph is a DAG. Also, you can assume that G contains no negative-weight cycles.
– two vertices x, y ∈ V .
• OUTPUT: distG(x,y)

The Problem: Write pseudocode for an algorithm that solves the above problem in O(|E|) time. For this problem, you MUST use graph transformation. In particular, you must run the algorithm DAG-SP(H,s) as a black box; this algorithm takes as input a DAG H = (VH, EH) and a source s ∈ VH and outputs distH(s,v) for all vertices v ∈ V ; DAG-SP runs in time O(|EH|). You are not allowed to modify this algorithm or rewrite it from scratch. The whole point is to use DAG-SP(H,s) as a blackbox to solve the above problem.

NOTE: you cannot run DAG-SP(G,s) because G is not a DAG! That’s why you need to use graph transformation.

NOTE: the solution I have in mind runs DAG-SP more than once. Also, note that you may run DAG-SP from any source.

WHAT TO WRITE: you need to write pseudocode for your algorithm, and whenever you run DAG-SP(H,s) make that’s that it’s very clear from your pseudocode what your graph H is and what the source s is.

中文版本：

G = (V, E)是一个有向的加权图（边的权重允许是负的）。对于任何边S⊂E的子集，我们用G-S=（V，E-S）表示去除S的所有边的图G。

  • INPUT:
    • 一个有向加权图G（边的权重允许为负），以及一条边（a，b），使得G- {（a，b）}是一个DAG；也就是说，如果你从G中移除边（a，b），那么得到的图是一个DAG。另外，你可以假设G不包含负重的循环。
    • 两个顶点x，y∈V。
  • OUTPUT：
    • distG(x,y)

问题：为一个能在O(|E|)时间内解决上述问题的算法编写伪代码。对于这个问题，你必须使用图转换。特别是，你必须将DAG-SP(H,s)算法作为一个黑盒来运行；该算法将DAG H = (VH, EH)和源s∈VH作为输入，并为所有顶点v∈V输出distH(s,v)；DAG-SP运行时间为O(|EH|)。你不允许修改这个算法或从头开始重写它。重点是将DAG-SP(H,s)作为一个黑盒来解决上述问题。

注意：你不能运行DAG-SP(G,s)，因为G不是一个DAG! 这就是为什么你需要使用图转换。

注意：我心目中的解决方案是不止一次地运行DAG-SP。另外，请注意，你可以从任何来源运行DAG-SP。

写什么：你需要为你的算法写出伪代码，每当你运行DAG-SP(H,s)时，你的伪代码要非常清楚你的图H是什么，源s是什么。

思路

如何分析题目

​ 首先题目非常长对吧让人感觉不是很想看，我们简单解释一下，题目给出了一个有向加权图G，并且给你一条G中的边(a,b)，图G去掉后这个G就会变成一个DAG图，DAG图也就是一个有向有权无环图，这说明G本身有一个环对吧，然后去掉环里面的这条边(a,b)后G’是一个没有环的有向有权图，也就是DAG图。然后题目希望我们计算图G中给定两点x和y之间的最短路径，那计算最短路径的方法很多，但是这是有环图，对于一个有环图计算最短路的方法有什么呢，Dijkstra等等都可以，但是题目要求时间复杂度O(|E|)，并且提供了一个DAG-SP函数，这个函数其实就是spfa单源最短路径算法，他有什么用呢？这个函数就是可以帮你算G’这个DAG图里面，一个点到另一个点的距离，那我们现在的想法就是借助这个函数，利用x和y在去掉边(a,b)后的G’图中的距离，来得到原图G中的距离，这是我们的思路，但是空想我们很难受，我们先画个图看看。

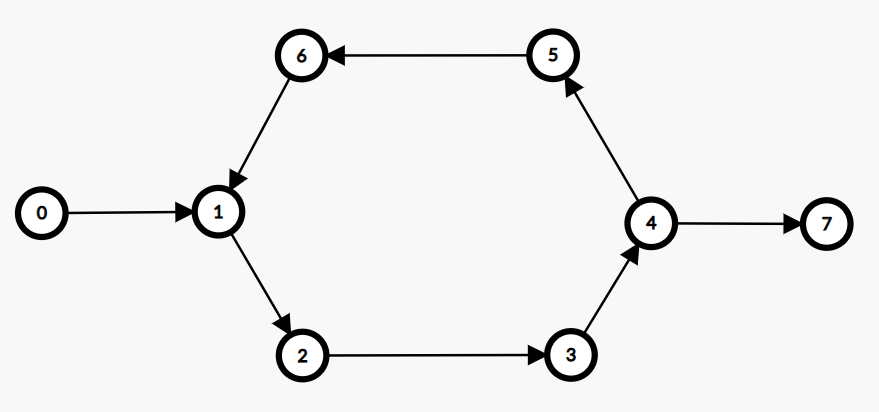
image-20220501214010190

画图分类讨论

​ 对于这个图，我们如果x和y取0和1，那ab去掉啥都无所谓对吧，反正去掉后的和去掉前的值会一样的。然后我们取x为0，y为7看看，这时候断掉的边(a,b)是哪条边就很关键了，如果(a,b)是(1,2),(2,3),(3,4)这3条之一(断掉的边一定在环上)，我们假设断掉(2,3)，那么断掉后的图G’中，0和7之间的距离的计算需要用0到2的距离加上2到3的距离加上3到7的距离，来计算。而如果是其他的边，那么断不断掉也不影响，原图G中的距离就等于G’中求出来的dist(0,7)，还有别的情况么？有的，如果要算环上两个点之间的距离呢？我们这次假设要求1到5的距离吧，那么断的边肯定在环上，这样的话1到5的距离能不能直接在G’中求出也要看(a,b)是否把我们原本可以走的路断掉了。

​ 从上面的分类讨论我们可以看出，(a,b)有没有断掉我们原来在图G中可以走的路非常关键，而且上面的图路径也比较少，要么是本来G中走得通被断掉，要么是本来G中走得通没被(a,b)断掉，并不存在(x,y)之间本来有两条路，如果之间本来就有两条路，被断掉一条，那么我们应该把两条分别算出来然后计算两条哪条最短，这也是我们的最终思路，就是计算被(a,b)断掉的路径(假设存在)和没被(a,b)断掉的路径(假设存在)中最短的那条路径，就是我们算法要求的内容，下面是具体的算法和伪代码

算法

我的算法是对图G’中的不同来源使用DAG-SP(G’,x),DAG-SP(G’,a),DAG-SP(G’,b)来得到distG’(x,y),distG’(x,a),distG’(x,b),,distG’(a,y),distG’(b,y)

对于xy之间没通过ab的路径：由于G’已经去掉了ab边，如果我们能通过DAG-SP(G’,x)得到distG’(x,y)，那么就意味着xy之间有一条不经过ab的路径，所以这个路径在图G中的长度是distG’(x,y)。

对于xy之间通过ab的路径：如果我们可以通过DAG-SP(G’,a), DAG-SP(G’,b)得到distG’(x,a)和distG’(b,y)或者distG’(x,b)和distG’(a,y)，那么就存在一条从x到y经过(a,b)的道路。对于经过a,b的路径长度是图G中的Min{distG’(x,a) + w(a,b) + distG’(b,y), distG’(x,a) + w(a,b) + distG’(b,y) }。（因为我们没法直接知道是x->a->b->y还是x->b->a->y）

因此，x和y之间的最短路径是distG(x,y)=min{distG’(x,y), distG’(x,a) + w(a,b) + distG’(b,y), distG’(x,a) + w(a,b) + distG’(b,y)}

伪代码实现

1
2
3
4
5
6
7
8
9
10
11
12
Function calcDist(G,a,b,x,y){
    //The algorithm assumes that if there is no pathway between two points, the be dist(a, b) is ∞
    // G− {(a, b)} is a DAG
    var H =  G− {(a, b)} ;
    //DistG'(x,y),distG'(x,a),distG'(x,b),distG'(a,y),distG'(b,y) are obtained using DAG-SP with x,a,b as sources respectively.
    distH(x,y),distH(x,a) = DAG-SP(H,x);
	distH(a,y)= DAG-SP(H,a);
	distH(b,y)= DAG-SP(H,b);
    //According to the above algorithm, the calculation can be obtained (x, y)
    distG(x,y) = Min{distH(x,y), distH(x,a) + w(a,b) + distH(b,y), distH(x,a) + w(a,b) + distH(b,y)}
    return distG(x,y);
}